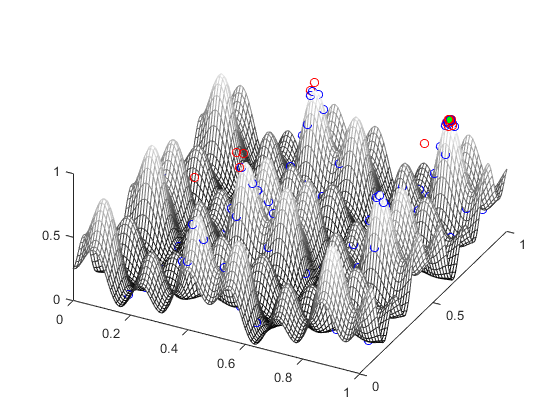
Main Input: a non-convex black-box deterministic function
Main output: an estimate of global optima
The form of the input function need not be known (black box) and thus a user can pass a function that simply calls, for example, a simulator as the input function.


The abstract of the paper that presented the method:
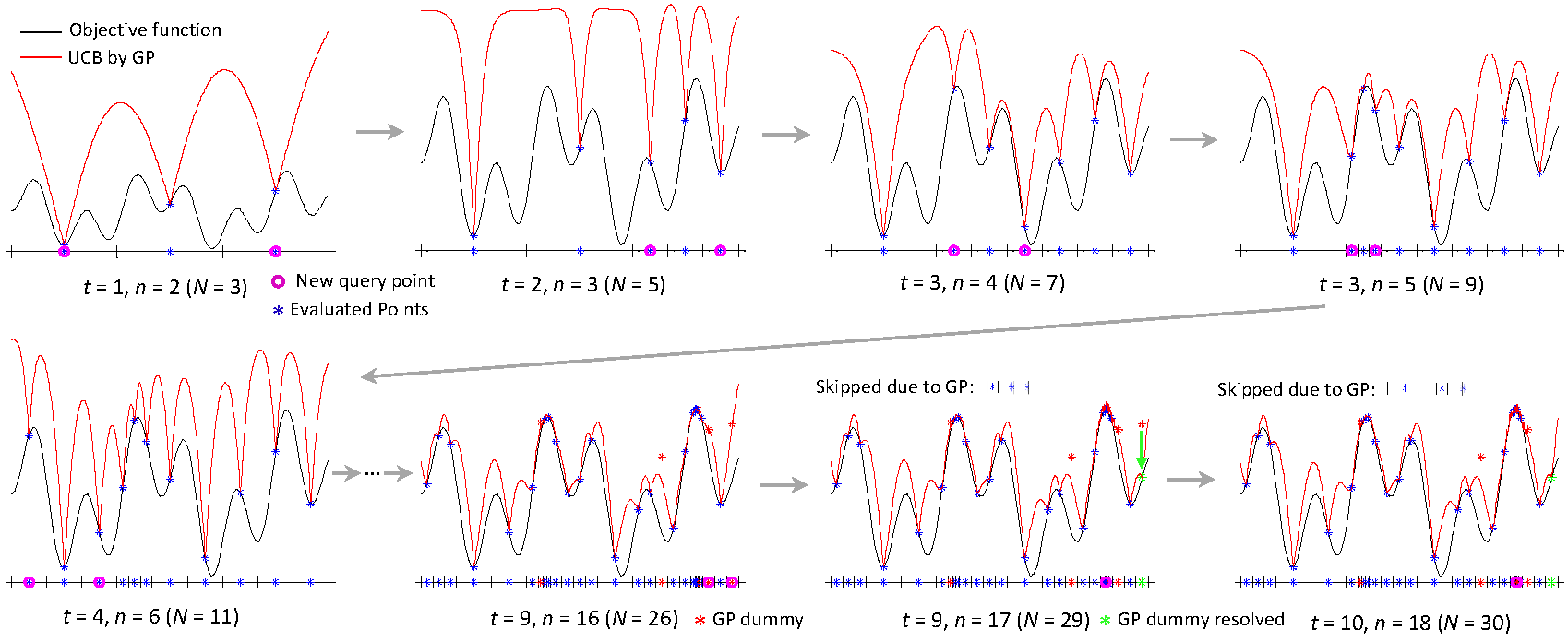
This paper presents a Bayesian optimization method with exponential convergence
without the need of auxiliary optimization and without the δ-cover sampling.
Most Bayesian optimization methods require auxiliary optimization: an additional
non-convex global optimization problem, which can be time-consuming
and hard to implement in practice. Also, the existing Bayesian optimization
method with exponential convergence [1] requires access to the δ-cover sampling,
which was considered to be impractical [1, 2]. Our approach eliminates both requirements
and achieves an exponential convergence rate. In our experimental
examples, the proposed algorithm outperformed previous methods by using fixed
parameter values that agree with our theoretical analyses.
For more information, please see the paper.